שטח מגרש הלווים

 מאת: אורן סעיד

לחישוב שטח מגרש הלווים, הגמרא נעזרת בכלל ההנדסי, שאם נחסום עיגול בתוך ריבוע – באותו רוחב של הריבוע - שטח הריבוע יהיה גדול משטח העיגול ברבע.

בפרשתנו אנו קוראים על הציווי להקצות ללווים ארבעים ושתיים ערים לנחלה להתיישב בהם, בנוסף לשש ערי המקלט; זאת מאחר, ולשבט לוי לא היה חלק בנחלת הארץ, נצטוו השבטים האחרים לתת לשבט לוי  מנחלתם, ארבעים ושתיים ערים. לכל עיר התורה מצווה להקצות גם מגרש אשר ישמש את הלווים לאיחסון רכושם, הבהמות ושאר החיות. התורה מפרטת את גודל המגרש: "וּמִגְרְשֵׁי הֶעָרִים אֲשֶׁר תִּתְּנוּ, לַלְוִיִּם מִקִּיר הָעִיר וָחוּצָה, אֶלֶף אַמָּה סָבִיב.  וּמַדֹּתֶם מִחוּץ לָעִיר, אֶת פְּאַת קֵדְמָה אַלְפַּיִם בָּאַמָּה וְאֶת פְּאַת נֶגֶב אַלְפַּיִם בָּאַמָּה וְאֶת פְּאַת יָם אַלְפַּיִם בָּאַמָּה וְאֵת פְּאַת צָפוֹן אַלְפַּיִם בָּאַמָּה וְהָעִיר בַּתָּוֶךְ; זֶה יִהְיֶה לָהֶם מִגְרְשֵׁי הֶעָרִים (לה, ד-ה).  כבר בקריאה שטחית, ניתן להרגיש בסתירה [1] לכאורה הקיימת בפסוקים. בתחילה התורה אומרת שצריך למדוד אלף אמה מחוץ לעיר עבור המגרש, ולאחר מכן התורה אומרת שצריך למדוד אלפיים אמה מחוץ לעיר. הכיצד?

במשנה במסכת סוטה, תירץ רבי אליעזר בן רבי יוסי הגלילי, שה"אלף אמה" הן לשטח המגרש, ואילו ה"אלפיים אמה" הן לשטח השדות והכרמים של העיר: "רבי אליעזר בנו של רבי יוסי הגלילי אומר: אלף אמה מגרש, ואלפיים אמה שדות וכרמים" (פרק ה משנה ג). מפני שרבי אליעזר בן רבי יוסי הגלילי, לא ציין את השטח הכללי של השדות והכרמים עם המגרשים, נוצרה על כך מחלוקת בין הפרשנים. רש"י מפרש: "אלף אמה סביב - ואחריו הוא אומר אלפים באמה, הא כיצד? אלפיים הוא נותן להם סביב, ומהם אלף הפנימיים למגרש והחיצונים לשדות וכרמים" (שם). סה"כ יש למדוד אלפיים אמה מחוץ לעיר, כאשר רק השטח של אלף האמות הקרובות לעיר ישמשו למגרש עבור הבהמות והחיות [2], ואילו השטח של אלף האמות החיצוניות ישמשו לזריעה, לשדות ולכרמים [3]. מקור דברי רש"י הוא בתלמוד בבלי מסכת עירובין: "תניא: אמר רבי אליעזר ברבי יוסי: תחום ערי לוים - אלפים אמה; צא מהן (רש"י - סביב העיר) אלף אמה מגרש (רש"י - שאין נוטעין ולא זורעין שם אלא מניחין אותו לנוי העיר, כדמתרגם 'וּרְוָחֵי קִרְוַיָא' [במדבר לה פסוקים ב,ד]), נמצא (שטח) מגרש רביע והשאר שדות וכרמים. מנא הני מילי (רש"י - דמגרש אלף אמה)? אמר רבא: דאמר קרא (במדבר לה,ד) [ומגרשי הערים אשר תתנו ללוים] 'מִקִּיר הָעִיר וָחוּצָה, אֶלֶף אַמָּה סָבִיב'; אמרה תורה: סבב את העיר באלף [4]" (עירובין נו, ב).

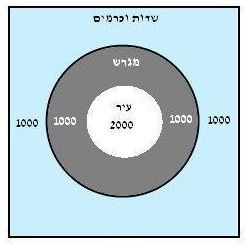
אחת האפשרויות לחישוב שטח מגרש הלווים.

"נמצא מגרש רביע"

רבי אליעזר ברבי יוסי בברייתא לעיל, ציין ששטח המגרש הוא רבע מהשטח של התחום כולו (העיר, המגרש והשדות והכרמים). הגמרא בעירובין (שם) מבארת במספר דרכים באילו מיקרים שטח המגרש יהיה רבע משטח התחום כולו. את האפשרות הראשונה, מעלה רבא, ומציין שמדובר בעיר עגולה שקוטרה 2000 אמות [5]. את העיר מקיף מגרש עגול (שהרי לא מצינו הלכה מיוחדת המצריכה לרבע את המגרש) ברוחב 1000 אמות מכל צדדי העיר. מכאן שקוטר המגרש יחד עם העיר הינו 4000 אמות. את העיר והמגרש מקיף התחום בצורת ריבוע (ישנה הלכה מיוחדת שאת התחום צריך לרבע [6]) של השדות והכרמים ברוחב של 1000 אמות מכל הצדדים. הרי שאורך רוחב ריבוע התחום (העיר עם המגרש והשדות והכרמים מסביב) הינו 6000 אמות. שטח התחום פשוט לחישוב: שטח הריבוע הינו 36,000,000 אמות (6000 X 6000) מרובעות [7]. מהו שטח המגרש?

על מנת לחשב את שטח העיגול של העיר והמגרש הגמרא נעזרת בכלל ההנדסי, המופיע במספר מקורות בחז"ל: "כמה מרובע יתר על העגול? רביע" (שם) כלומר, אם נחסום עיגול בתוך ריבוע – באותו רוחב של הריבוע - שטח הריבוע יהיה גדול משטח העיגול ברבע (בהמשך נדון בכלל זה). ע"פ כלל זה אם העיר היתה בצורת ריבוע שאורכו ורחבו 2000 אמות, שטחה היה 4,000,000 אמות מרובעות (2000 X 2000); על מנת לחשב את השטח של עיר עגולה שקוטרה 2000, ע"פ הכלל הנ"ל, עלינו להפחית רבע, כלומר 1,000,000 אמה. הרי ששטח העיר העגולה הינו 3,000,000 אמות מרובעות (1,000,000 - 4,000,000). באופן דומה, נחשב את שטח המגרש עם העיר, ונקבל שהשטח הוא  12,000,000 אמות מרובעות [16,000,000  - שטח הריבוע שחוסם את העיר והמגרש; משטח זה נפחית רבע -  4,000,000 אמות]. מכאן ששטח המגרש (ללא העיר) הינו 9,000,000 אמות מרובעות (שטח המגרש יחד עם העיר פחות שטח העיר: 3,000,000- 12,000,000) – שטח שהוא רבע מהשטח של התחום כולו[8] (36,000,000 אמות מרובעות, ראה תרשים).

"כמה מרובע יתר על העגול - רביע"

כלל זה מופיע במשנה במסכת אהלות: "וכמה יהא בהיקפה, ויהא בה פותח טפח:  בזמן שהיא עגולה, היקפה שלושה טפחים; ובזמן שהיא מרובעת, ארבעה שהמרובע יתר על העגול רביע" (יב, ו). התוספות בעירובין מציין שכלל זה, מרובע גדול מהעיגול ברבע, זה הן בהיקף והן בשטח: "כמה מרובע יתר על העגול רביע – ואומר ר"י דהא רביע בין בהיקף בין בגוף הקרקע" (שם).

היקף העיגול והריבוע

התוספות (עירובין, שם) מביא הוכחה לכך שהיקף הריבוע גדול ברבע מהיקף העיגול (החסום על ידי הריבוע), מהכלל ההנדסי בתלמוד ליחס שבין היקף העיגול לקוטרו - "כל שיש בהיקפו שלשה טפחים - יש בו רחב טפח", כלומר היקף העיגול גדול פי שלושה מקוטרו. מכאן, עיגול שקוטרו טפח היקפו שלושה טפחים ואילו ריבוע שאורכו ורחבו טפח היקפו ארבעה טפחים, הרי שהיקף הריבוע גדול ברבע (טפח) מהיקף העיגול (החסום על ידי הריבוע).

הגמרא בעירובין לומדת את הכלל של היחס שבין היקף העיגול לקוטרו, מהמידות של הים של שלמה (=כלי קיבול גדול של מים, שעשה שלמה בבית המקדש), שההיקף שלו (30 אמות) היה גדול פי שלושה מהקוטר שלו [9] (10 אמות): " מנא הני מילי? אמר רבי יוחנן: אמר קרא (מלכים א ז, כג) 'וַיַּעַשׂ אֶת הַיָּם מוּצָק עֶשֶׂר בָּאַמָּה מִשְּׂפָתוֹ עַד שְׂפָתוֹ עָגֹל סָבִיב וְחָמֵשׁ בָּאַמָּה קוֹמָתוֹ וְקָו שְׁלֹשִׁים בָּאַמָּה יָסֹב אֹתוֹ סָבִיב (רש"י - משפתו עד שפתו - חללו שלו, לבד עובי דופנותיו = עשר אמות, וכתיב וקו שלשים באמה יסוב אותו אלמא: לכל אמה רוחב בעיגולא איכא שלש אמות היקף)" (ערובין יד, א).  יש לציין, שהיחס בין היקף המעגל לקוטרו הוא  Л (פאי) שערכו בקירוב -  3.1415926536, וכבר העירו על כך התוספות [10]: "משמע שהחשבון מצומצם... וקשיא דאין החשבון מדוקדק לפי חכמי המדות" (ערובין יד, א ד"ה והאיכא משהו).

שטח העיגול והריבוע

בתוספות (שם) מוכיח ר"י (רבינו יצחק, מבעלי התוספות) ששטח הריבוע גדול ברבע משטח העיגול (החסום על ידי הריבוע). ר"י מחשב את השטח העיגול  שקוטרו טפח אחד כך:

נקיף את מרכז העיגול במעגלים עשויים חוט דק באופן שיכסו את שטח העיגול (הציור העליון), נחתוך אותם לאורכו של רדיוס אחד (הרדיוס האדום שבציור), וניישר את החוטים (הציור התחתון). הגובה המסומן בציור התחתון הוא הרדיוס שבהמשך רדיוס החיתוך שבציור העליון. יישור החוטים נעשה באופן שהנקודות שעל הרדיוס הזה תישארנה במקומן והחוטים יישארו ניצבים לרדיוס זה. כך מתקבל משולש שבסיסו שלושה טפחים (היקף העיגול)  וגובהו חצי טפח [11] (רדיוס העיגול, השווה לחצי מקוטר העיגול), לכן שטחו הוא 3/4 טפח מרובע (בסיס כפול גובה חלקי 2); ואילו שטח ריבוע שצלעו טפח הוא טפח מרובע (אורך כפול רוחב). הרי ששטח העיגול גדול ברבע (רבע טפח) משטח הריבוע שבאותו רוחב [12].

---

[1]  השד"ל יוצא חוצץ נגד תרגום השבעים, שתיקן בפסוק ד' "אלף" ל"אלפיים".  השד"ל מתרץ בעצמו את הסתירה בין הפסוקים כך: "והנה כבר הראיתי ב"בכורי העיתים" תקפ"ט (עמוד קיד) כי באמת אין שני הכתובים האלה סותרים זה את זה, כי באחד כתוב מקיר העיר וחוצה, ובאחד כתוב מחוץ לעיר, והנה המגרש היה נמשך אלף אמה מחוץ לחומה, אבל מחוץ לעיר כלומר מחוץ לבתים היה אלפים אמה, כי כמו שהיו מניחין מקום פנוי בלי בתים לפנים מן החומה; והמנהג הזה מצאנוהו אצל הרומאים בתחילת הוייתם, כי רומולוס בבנותו עיר רומי הניח מקום פנוי קצתו מן הבתים אל החומה אשר לא ייבנה בו, וקצתו מקיר העיר וחוצה, אשר לא ייעבד בו ולא ייזרע" (לה, ד-ה). מחומת העיר היה המגרש אלף אמה, אבל מהבתים, בשל הרווח בין החומה לבתים, היה המרחק אלפיים אמה.

[2]  שטח פתוח, שאין זורעים או נוטעים שם, לנוי העיר (ראה רש"י ערובין נו, ב – בהמשך המאמר).

[3] רש"י וכן רבינו עובדיה מברטנורא, מפרשים את דברי רבי יוסי הגלילי "אלפיים לשדות וכרמים" = השאר לשדות וכרמים – כפי לשון הברייתא בעירובין (נו, ב) - ולא שכל שטח השדות הכרמים הוא אלפיים אמה.

[4] לעומת זאת, לדעת הרמב"ם, אורך מגרשי ערי הלויים היו במרחק של עד שלושת אלפים אמה מהעיר עצמה, מתוכם אלף האמה הסמוכות יותר לעיר שימשו כמגרש, ואילו אלפיים האמה החיצוניות יותר שימשו כשדות וככרמים[4] (הלכות שמיטה יובל, פרק יג הלכה ב).

[5] אמה היא יחידת מידה קדומה לאורך, שיעורה 48 ס"מ לפי שיטת רבי חיים נאה.

[6]  על מנת שיהא נשכר בקרנות, באלכסון, ראה עירובין נו, ב.

[7] אמה מרובעת, הכוונה לשטח ריבוע שאורך צלעו אמה אחת.

[8] גם אביי מתרץ,  שמדובר בעיר עגולה ומגרש עגול, והגמרא שוב משתמשת בכלל "כמה מרובע יתר על העגול? רביע" (שם), אלא שמתרץ שמדובר בעיר בקוטר אלף אמה וכן המגרש  מקיף את העיר סביב אלף אמה, ואז שטח המגרש הוא רבע משטח התחום כולו – אבל ללא שטח העיר. אנו הבאנו את התירוץ הראשון שמופיע בגמרא שהוא של רבא.

בנוסף, צורת החישוב בגמרא היא קצת שונה ממה שהצגנו כאן (אבל התוצאה זהה) והיא מחלקת את כל השטח לריבועים של אלף אמה על אלף אמה, כי היא מציינת מהו שטח "תחום שבת" ומהו שטח הקרנות. לשם פשטות החישוב, והצגת הנושא העיקרי של המאמר,  שהוא הדגמת הכלל "כמה מרובע יתר על העגול? רביע" (שם), הצגנו את החישוב הישיר ללא צורך החלוקה לריבועים.

לסיכום שיטות "תחום ערי הלויים" בסוגיא במסכת עירובין (שם) ראה בפורטל הדף היומי.

[9] תיאור זה, לכאורה, עומד בסתירה לעובדה שהיחס במעגל בין הקוטר להיקף הוא פאי: המתחיל בספרות ...3.14159, ואילו היחס המתואר בתנ"ך הוא 3 (30 ל-10). המתבוננים בגימטריה של הטקסט יבחינו כי השימוש בכתוב במילה קוה (בגימטריה 111) מתוקן על ידי הקרי למילה קו (בגימטריה 106). אם נחלק 111 ב-106, נקבל 1.04716981, ואם נכפיל תוצאה זו ב-30 (ההיקף כפי שמתואר בכתוב) נקבל 31.4151, כלומר קירוב עד עשירית המילימטר של ההיקף האמיתי. יש מן המפרשים האומרים שהמספר האמור במקרא הוא מספר עגול. הסבר אחר תולה את ההפרש בעוביו של הים - הקוטר נמדד מהדפנות החיצוניות, ואילו ההיקף סביב הדפנות הפנימיות.

[10] ראה גם פירוש המשניות לרמב"ם, עירובין פרק א משנה ה ; ראה גם בשו"ת תשב"ץ חלק א סימן קסה, שלכן הביאה הגמור מקור (פסוק) ללמוד ממנו את היחס בין היקף העיגול לקוטרו, ולא הסתמכה על הידע המתימטי שרווח בתקופתם, כדי להורות שבחישובים הלכתיים יש להשתמש בערך המקורב לפאי - שלוש, ולא בערך המדוייק של פאי.

להרחבה ראה במאמר "מספרים אי רציונאליים בפרשה ובחז"ל", בפרשת תרומה.

[11] ר"י אינו מסביר מנין לו שאחרי ישור המעגלים יוצרים קצות החוטים שוקיים ישרות. הדבר יכול להתקבל מזה שההיקפים של מעגלי החוטים פרופורציוניים לרדיוסיהם, לכן אורכי החוטים הישרים פרופורציוניים למרחקיהם מהקדקד.

[12]  ראה גם מאמרו של פרופ' עמוס ארליך, החוג להוראת המדעים, אוניברסיטת תל-אביב, "כמה מרובע יתר על העיגול רביע", תשס"ה, 2005, באתר "דעת", מכללת הרצוג.

הוכחה זהה בספרו של רבי אברהם בר חייא הנשיא (המאה ה-12) "חיבור המשיחה והתשבורת", בחלקו השני של הספר. המחשה לנוסחת שטח המעגל ע"פ אברהם בר חייא מובאת במאמר "The proof of Rabbi Abraham Bar Hiya Hanasi " מאת בועז צבאן ודוד גרבר, אונ' בר-אילן.

© כל הזכויות שמורות למחבר